Conventional approach to PDE solvers is to use independent discretizations in space and time. However, in some cases of complex dynamics this may lead to the inability of the mesh to adapt to the deformations of the objects and the domain, i.e. flapping wings, rotational motion, etc.. Especially difficult are the problems involving objects undergoing topological transformations as, for example, in cell mitosis. But even a simple motion can be difficult to handle with an adaptive mesh when the deformations become too strong. This leads to the necessity of periodical re-meshings, which in turn causes accuracy losses associated with interpolations, and degrades the performance.
A method proposed here uses space-time meshes which resolves these issues. The solution of dynamic problems on such meshes turns into static solutions on a four-dimensional domain. This opens a possibility of extending conventional implicit iterative solution schemes to 4D explicit schemes providing a solution in space-time by successive approximations and mesh refinements from the initial conditions. A further extension to fully implicit 4D schemes is also possible.
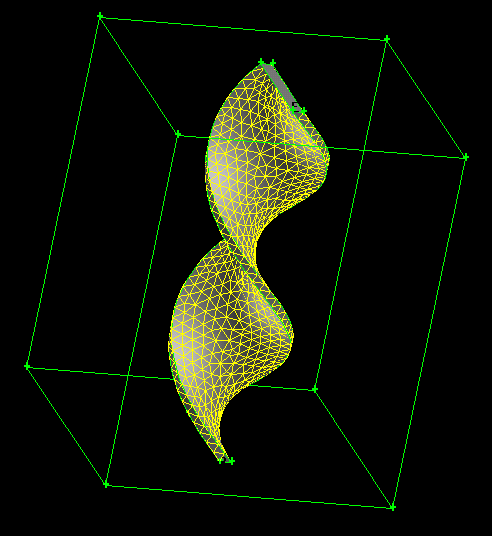
Consider an example of a rotating propeller. If one uses a non-rotating frame of reference, which often is the only option, then it becomes practically impossible to keep the mesh consistent after already 90° turn of the propeller, nothing to say about a complete revolution. On the other hand, if one implemented the dicretization using space-time elements, such as 4D pentagons instead of 3D tetrahedrons, then one would in principle be able to represent the complete revolution of the propeller with a single continuous mesh. To illustrate this idea, let's consider revolution of a 2D object in the plane. For simplicity, consider a rectangle rotating in a plane. Then the space-time region describing this motion will be a 3D domain, and the motion itself will be represented as a spiral object in this domain, as shown in the figure.

After we mesh the space-time region with a tetrahedral mesh we obtain the space-time discretized domain of the whole event of propeller revolution. The mesh will adjust smoothly to the surface of the spiral and no inconsistencies will be caused by the rotation. To obtain the solution to fluid motion in this case the equations have to be discretized in a manner consistent with the space-time elements of the mesh.
Another advantage of space-time discretization is that it enables to use different time-scales in different regions of space-time. Thus, if the process occurs rapidly in one region of space and there is little activity in another region (explosions, jets, etc.), the space-time mesh can reflect this by applying a finer discretization in both space and time in the region of rapid process and using a coarse mesh in stagnant areas.
A CFD solver based on this idea, Flow4D, is currently under development.