There were two tasks to be solved for an efficient implementation of an LPD procedure: (1) particle tracking and (2) particle population dynamics. The first task is related to the problem of identifying the grid-cell where the particle is located, and interpolating the relevant grid-based variables to the particle location. The second task is related to the problem of creating and destroying particles as the need arises due to the processes of particle injection, disappearance through the free surface and crossing the boundaries of the computational domain. Since both particle tracking and population control are frequently occurring operations, it would be highly desirable to solve each task in a manner that would avoid expensive loops through the particles or grid-node arrays.
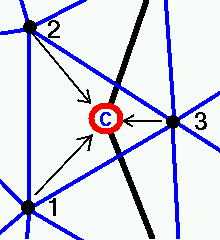
When the particle tracking is done on structured grids, the location of the grid-cell containing the particle is a straightforward task reduced to a division-by-modulus, multiplication and addition operations. When non-uniform or unstructured grids are used the procedure is not as simple. In this case there should be a way to identify if the current location of the particle is inside the same cell it was inhabiting in the previous iteration or whether the particle has moved into a neighboring cell see Figure below.
The present LPD procedure accomplished this task by solving the inclusion problem in a polyhedron. This is a standard algorithm in the area of computational geometry, where the given point is tested against each face of a polyhedron and it is decided if the point is on the inside or the outside of the face relative to the center of the polyhedron. In the end the point is either found to be inside the polyhedron or the search is repeated in the neighboring polyhedron lying across the first face, which failed the test. Identification of the neighboring cells is a simple matter on structured grids, whereas on unstructured ones a cell-cell connectivity information should be used.
The inclusion problem is solved by analyzing the scalar product between the face normal vector and the vector connecting one of the face-nodes to the particle:
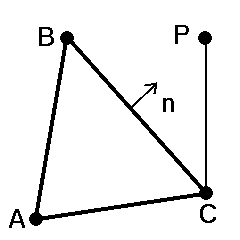
If this product is positive the point lies across the face, otherwise it is on the inside of the face. If the product is negative for all faces the point is inside the cell. The inclusion problem algorithm is used in a loop to to locate the next host-cell for a particle inside the mesh:
next=cell;
While(next!=NULL)
{ if((next=HostCell(cell,x))==cell)
break;
cell=next;
}
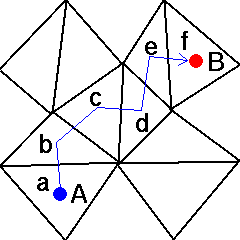
The HostCell function above has as input the pointer to the current cell, and the coordinates of the point: x[0], x[1], x[2]. The function returns the pointer to the same cell if the point was found inside that cell or the pointer to the neighbor cell if the point was located across the face to that neighbor cell. It returns NULL if the point was found to lie across the boundary face. The loop above will terminate either when the host-cell is found or when the boundary of the domain is reached. This is a faster serach than exhaustive testing of all cells on the inclusion, since its execution time will be linear in the distance separating the previous and the new point, as illustrated in the figure below:
Finally, the linear interpolation is used to obtain the continuum variables defined at grid nodes at the given point inside the host-cell:
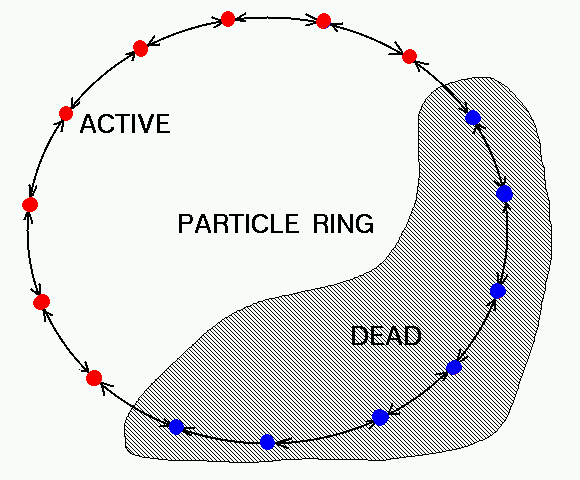
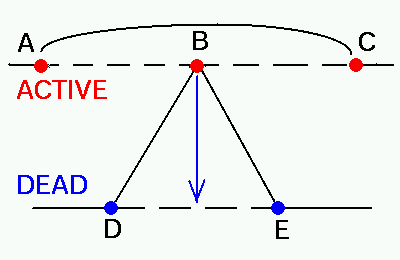
For an efficient implementation of particle population control algorithm, it would be desirable to avoid both looping trough the particles and dynamic memory allocations/deallocations in cases when new particles are created or destroyed. It can be achieved by using linked lists. In the present scheme an array of the size equal to the maximum number of particles is initially allocated. Then the pointer system is setup to link all the particles together in a ring fashion, separating them into active and dead sublists (see Figure). Whenever a particle is created or destroyed it takes only six pointer assignment operations to move it between the active and dead sublists. Figures below shows an example of destruction of particle B by the appropriate reassignment of pointers between the old neighbor-particles A,C and the new ones: D,E.
Even though the limitation on the maximum number of particles in the domain may seem restrictive, it is a compromise, allowing to avoid dynamic allocation/ deallocation of memory space for each newly created or destroyed particle. Since the latter operations can be rather frequent this procedure seems reasonable from efficiency standpoint.