[Line segment AB, intersecting the boundary between two objects at point C.]
These part of the code contains implementation of a problem-specific data structures and algorithms. In addition to the basic domain data model of the kernel the models introduce new data types and associated methods (algorithms).
There are currently two types of models that can be implemented outside of the kernel: plugin models and server models. Plugin models are implemented and executed directly in the client code running locally on user's workstation. Server models are implemented on a remote computing facility (Beowulf cluster) but are setup and started from the client.
Plugin models can be used for complex data initialization and pre-processing that can be needed on the client side. They can also be used as stand-alone models for problem specific solutions. Each plugin model consists of Data structures and Methods. The user interface to the models consists of Initializer and Iterator. Usually both are either implemented by the user or supplied as additional modules to the kernel. Both initializer and iterator are invoked by separate buttons on the control panel. The following plugin models are currently available.
These models allow representation of surfaces of different component objects in a grid-independent manner. Usually the "raw" surface represented by pixels retains the unisotropy of the underlying grid. A grid-independent triangulated mesh of this surface can be created by applying advanced meshing techniques and/or surface transformations.
The following methods can be applied to generate and manipulate the boundary data structures described above:
The boundary data can be rendered using several rendering modes:
The method described here will enable one to convert a pixel-based representation of the geometry to a representation based on a connected set of geometrical elements (cells, faces, edges, nodes). The size of the elements is usually greater than the size of a single grid-pixel.
The method is based on a Generalized Element Method (GEM) currently being developed as a part of MulPhys multi-physics modeling framework (paper 1, paper 2, paper 3) and represents a valuable extension to the geometrical modeling since it links pixel-graphics representation of the geometry to the control-volume representation required for the physical modeling.
The basic kernel geometry model is based on pixel-graphics. This opens possibility to use very simple and versatile geometry modeling tools. However, the size of a pixel may be prohibitively small for modeling complex physical processes on a large scale. For these purposes a sub-division of space into control-volumes is usually employed. In this method the space is subdivided into cells of arbitrary shape and physical variables are assigned to each cell in a manner that will provide a certain degree of continuity of the variables inside the cell and at the cell boundaries. A cell it typically represented by a polyhedron, and depending on the placement of a variable inside the cell the variable may be node-based, edge-based, face-based or central. Considering this, it is convenient to introduce a generalized element (GE) as a geometrical primitive of a variable dimension, d: node (d=0), edge (d=1), face (d=2) and cell (d=3). The elements of higher dimension can include elements of lower dimension and those of lower dimension can belong to those of higher dimension. The number of lower dimensional elements that a higher dimensional element includes will determine its order. Each variable is then considered to be defined to one particular element type.
The physical laws are then formulated as a system of algebraic relations between the variables defined on different elements, which is called the discretization scheme. Since most of the physical laws obey some locality property, these relations usually span only the neighboring elements. In this case the matrix of the discretization scheme, determining the relationships between the variables, is characterized as sparse. If the physical laws are given in a partial differential form, as is often the case, the discretization scheme is obtained by application of finite-element, control-volume or finite-difference discretization methods. If the law is given in an integral form or as a low-dimensional analytical solution (2D duct flow, surface electro-chemistry, etc.), the discretization scheme can simply be obtained as an interpolation of the solution to the set of elements. Following this approach, one can realize a general multi-physics modeling, which combines complex PDE solvers, and simple analytical approximations in a single framework.
To adopt the GEM approach one needs to be able to convert the pixel-based representation of the geometry, provided by the kernel model, into a generalized element representation. In other words one needs to establish a mapping between the objects in the pixel space and those described by the space of nodes, edges, faces and cells. Generally, a mapping from the pixel-space to the space of vectorized objects, such as those used in vector graphics, can be established as well.
It should be noted that the problem of mapping from the course-grained representation in the GE space to the fine-grained representation in the pixel-space is almost a trivial task. This is because it can be reduced to the inclusion problem, which is relatively simple, and has a unique solution when the pixel size is much smaller than the cell-size. On the other hand, the problem of subdivision of a pixel-space into generalized elements is not unique. Formally, it can be reduced to an optimization problem, but the solution can be combinatorially complex. A faster solution can be achieved by using heuristic methods where the user supplies some information on the type of elements that are desired in certain regions of space. For example, if the system contains a network of linear structures (optical fiber, struts, air/fuel ducts, etc.) a user can restrict the type of the element to be used on these structures to edges only. This will simplify the mapping procedure.
It is clear however that in this approach the graphical user interface should be extended with the possibility of defining point-like, linear and surface objects. The latter has been partially accounted for in the existing system by several models of the wireframe surface meshing. These models provide the way of defining pixel-independent representation of surfaces, and can be readily used to define surface elements. Realization of node-like elements is almost trivial, as long as each of these can be associated with a single pixel in the pixel-based representation.
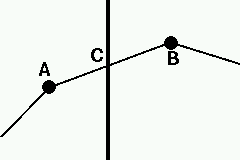
For linear elements line drawing module of the GUI is used. In this module each line is represented as a connected set of segments. When the line element mode is on, each line is stored as a linked list of objects, each object containing information on one segment of the line. This information includes pointers to the end-nodes of the segment (points A and B in the figure), cross-sectional area, as well as pointers to the nodes inside the segment, which correspond the boundary points of different objects that the element may cross (point C in the figure).

In this way it is possible to account of the interface areas between each line segment and the neighboring objects. This information is essential to account for fluxes of conserved quantities in the system (mass, heat, etc.).
Server models are separate programs compiled and executed on a remote Beowulf cluster. They should include interface modules to communicate with the remote master-gui (RING).
This is a currently used proprietary model for simulations of fuel-cell stacks (NETL/WVU). It was modified to include the module for reading the command and monitoring information from the master-module (GUI).