
The proposed approach of simulating flows in blood vessels, lung airways or bone capillaries is based on joint application of three well known methods
A CFD solver for unsteady Navier-Stokes (NS) equation will be used for a detailed flow modeling on different length-scales: from macro to capillary systems. Considering the bifurcating nature of biological flow passages (ducts), detailed simulations will have to be performed for each level of branching and later used to reproduce the total flow pattern by employing the appropriate fractal model of the ducts combined with the pipe-network solution methods. Thus, in order to span a range of scales from 1cm down to 1µ, assuming for simplicity a constant branching factor equal to 1:3 (the ratio of the cross-sectional areas of two branches at each bifurcation), a total of
n = 4*ln(10)/ln(1.5) = 23
detailed NS simulations will be required. For a symmetric branching this number will be reduced to 14.
The results of each simulation will be fed in to the pipe network algorithm that will be applied to the bifurcating fractal duct system. The maximum number of ducts will correspond to a symmetric branching factor and will be equal to
14
2 = 16384
Taking into account a uni-directional bifurcating pattern of the network, this system can be efficiently solved on a distributed memory computer platform, such as a cluster of workstations.
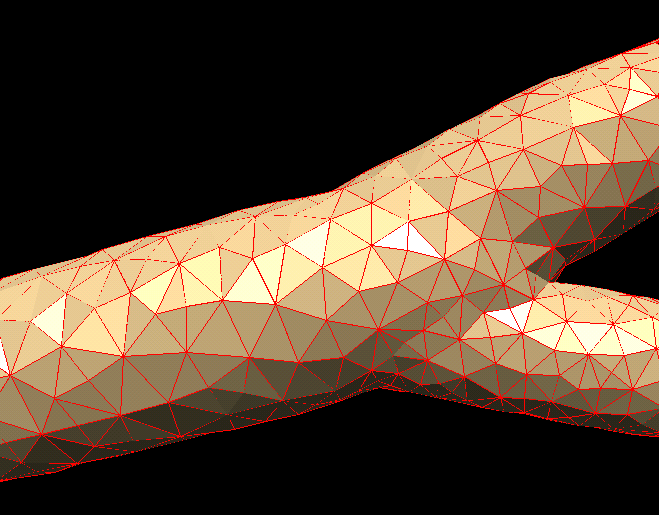
To compute the flow on a one level of a branching network a special control-volume/finite element fluid dynamic solver, Hedra will be used. Preliminary simulations of flow in a single branch have already demonstrated the feasibility of the method. The figures below show the flow pattern in a simple bifurcating passage with the pressure-specified inlet and outlet conditions.
Geometry of a single bifurcation and flow pattern obtained with the Hedra solver


In the simulation above the flow was driven by a constant pressure drop between the inlet and two outlets of the duct. Wall-friction effects were considerd.
Figures below show the simulated particle dynamics inside the bifurcating duct with wall-deposition. Steady and unsteady flow regimes, including flow reversal are considered.
[100 particles in unsteady flow.]
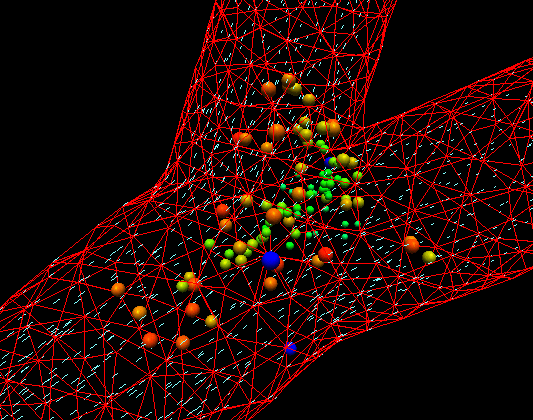
Animation
(5MB)
[1000 particles in steady flow. Side view.]

Animation: (20MB)
[Inside view]
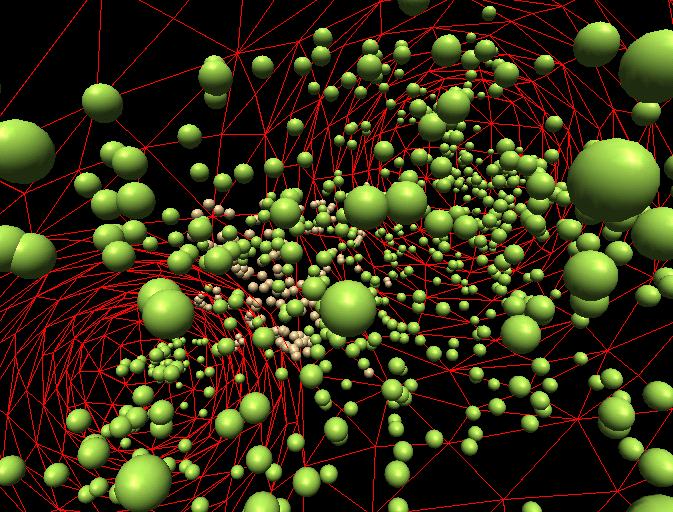
Green: free particles, brown: deposited on the walls.
Animation (6.5MB)
The overall macro-scale structure of the biological flow system will be reproduced using a fractal geometrical model of a tissue with the blood-vessel branching going through many levels of bifurcations and spanning a realistic range of scales from macro to capillary structures.

A simulated fractal tree shows 10 levels of branching with a symmetrical equal length splitting. More complex splitting schemes can be easily modeled as well.
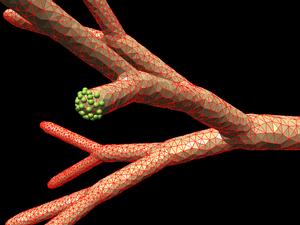
Animations: tissue growth, branching.
Recently developed new technique of dynamic gridding is specifically aimed at handling flexible boundaries and fluid-structure interactions in the context of biological flows.
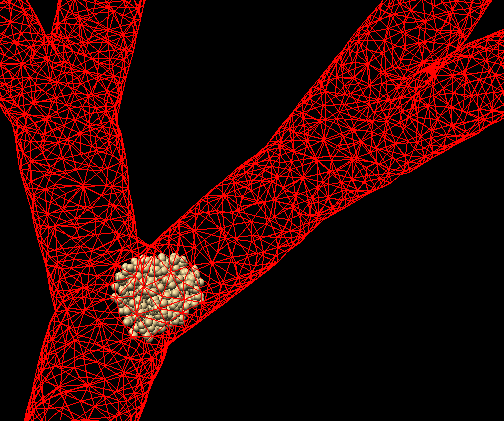
The figure above shows the snapshot of a prototype model of arterial
clogging. It demonstrates the potential of this technique in handling
complex biological flows. The complete animation can be seen
here.