In this study we propose a computational technique that does not require to keep track of the neighboring particles and completely avoids expensive looping over neighbor-particles subsets. Interaction between the particles is realized through the Eulerian grid used by the flow-solver. Here the idea is exploited that it is much simpler computationally to maintain the connectivity information between each particle and the surrounding grid nodes, than between each particle and the surrounding particles. Since each particle constantly keeps track of the neighboring grid nodes, as it moves inside the grid, accessing these nodes requires only a fast pointer reference operation.
Using this connectivity, one can arrange an inter-particle interaction in two stages. In the first stage particles interact with the neighboring grid nodes, exchanging momentum, mass, and other quantities, depending on the interaction mechanisms involved. As a result the grid nodes will receive the quantities lost by the particles, or the particles will "borrow" some quantities from the grid. The exchanged quantities are of a virtual nature since the grid has no physical reality. In the second stage another interaction between the grid and the particles is played, in which the virtual quantities are retrieved from the grid nodes and returned back to the particles so as to keep the total balance of conserved quantities like mass, momentum, energy etc. Since different particles may be engaged in the interaction with the grid nodes in the first and second stages, the complete process results in some redistribution of the quantities among the particles. With the appropriate choice of the virtual interaction law the actual interaction between the particles can be reproduced.
(b) Probabilistic implicit interaction
Figure1 present the comparison between the
conventional and the proposed interaction schemes. Here
,0,1 designate particles looping over the complete
particle set, is the neighboring grid node and is a
random number generated from the appropriate probability
distribution. The grid-node selection with function GridNode
does not involve any looping over the nodes, since the particle
carries the information on the current cell it is in and its
vertexes (grid-nodes). The essential feature of the new scheme
is the mechanism by which a grid-node can "borrow" and then
return back various properties of the particle. Since the
borrowed quantities may be of either negative or positive sign,
the term "borrow" would actually mean either "borrow" or "lend",
depending on the sign. In contrast to the common deterministic
interaction algorithm which is realized as two nested loops over
the particles (Fig.1a), and which we call an
explicit interaction scheme, the described procedure, which we
call a probabilistic implicit interaction scheme, is
realized in two sequential loops (Fig.1b), corresponding
to the two stages of virtual interaction with the grid.
Accordingly, the execution time of the algorithm is linear in
the particle number, whereas the algorithms based on direct
particle-particle interaction are worse than linear - usually
quadratic (Fig.1a), or maybe slightly better when space
subdivision is introduced to keep the particle-particle
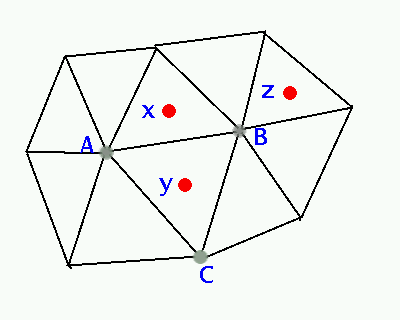
connectivity information local The technique is realized on a vertex-centered triangular grid
with overlapping control volumes, which is also used for the
solution of Navier-Stokes equation with a control-volume method
[{Ferziger and Peric, }{1997}]. This choice of grid precludes the blockage of
interactions between the particles located on different sides of
a grid-cell face, like particles (x,y) in Fig.2.
In this example the grid node A in the figure is
engaged in virtual interaction with particles (x,y), node B
with particles (x,y,z) and node C with particle y.
Consequently, interaction between the particles (x,y) can
occur via nodes A and B, whereas the interaction between the
particles (x,y) and (y,z) can only occur via node B.
In the scheme above the interaction range that can be handled by
the method will be limited by the size of a local
control-volume. However, it would be possible to eliminate this
grid-sensitivity by introducing an appropriate mechanism of
virtual interaction between the grid nodes themselves. This may
involve formulating a diffusion-like process, by which virtual
quantities stored at each grid-node would be transported to the
neighboring grid-nodes and so on. In this way the exchange of
quantities between the particles will not be limited by the
local control-volume sizes.
for (p0=pfirst..plast)
for (p1=pfirst..plast)
Interaction(p0<->p1)
(a) Deterministic explicit interaction
for (p=pfirst..plast)
{ g=GridNode(p);
if (R<InteractionProbability(p,g))
Borrow(g>-p);
}
for (p=pfirst..plast)
{ g=GridNode(p);
if (R<PayBackProbability(p,g))
PayBack(g->p)
}
